散列表(Hash table,也叫哈希表),是根据键(Key)而直接访问在内存储存位置的数据结构。也就是说,它通过计算出一个键值的函数,将所需查询的数据映射到表中一个位置来让人访问,这加快了查找速度。这个映射函数称做散列函数,存放记录的数组称做散列表。
一个通俗的例子是,为了查找电话簿中某人的号码,可以创建一个按照人名首字母顺序排列的表(即建立人名{\displaystyle x}到首字母{\displaystyle F(x)}的一个函数关系),在首字母为W的表中查找“王”姓的电话号码,显然比直接查找就要快得多。这里使用人名作为关键字,“取首字母”是这个例子中散列函数的函数法则{\displaystyle F()},存放首字母的表对应散列表。关键字和函数法则理论上可以任意确定。
基本概念
- 若关键字为
{\displaystyle k},则其值存放在{\displaystyle f(k)}的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系{\displaystyle f}为散列函数,按这个思想建立的表为散列表。 - 对不同的关键字可能得到同一散列地址,即
{\displaystyle k_{1}\neq k_{2}},而{\displaystyle f(k_{1})=f(k_{2})},这种现象称为冲突(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数{\displaystyle f(k)}和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。 - 若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
构造散列函数
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快定位。
- 直接定址法:取关键字或关键字的某个线性函数值为散列地址。即
{\displaystyle hash(k)=k}或{\displaystyle hash(k)=a\cdot k+b},其中{\displaystyle a\,b}为常数(这种散列函数叫做自身函数) - 数字分析法:假设关键字是以r为基的数,并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。
- 平方取中法:取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况,取其中的哪几位也不一定合适,而一个数平方后的中间几位数和数的每一位都相关,由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
- 折叠法:将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址。
随机数法 - 除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即
{\displaystyle hash(k)=k\,{\bmod {\,}}p},{\displaystyle p\leq m}。不仅可以对关键字直接取模,也可在折叠法、平方取中法等运算之后取模。对p的选择很重要,一般取素数或m,若p选择不好,容易产生冲突。
处理冲突
为了知道冲突产生的相同散列函数地址所对应的关键字,必须选用另外的散列函数,或者对冲突结果进行处理。而不发生冲突的可能性是非常之小的,所以通常对冲突进行处理。常用方法有以下几种:
- 开放定址法(open addressing):
{\displaystyle hash_{i}=(hash(key)+d_{i})\,{\bmod {\,}}m},{\displaystyle i=1,2...k\,(k\leq m-1)},其中{\displaystyle hash(key)}为散列函数,{\displaystyle m}为散列表长,{\displaystyle d_{i}}为增量序列,{\displaystyle i}为已发生冲突的次数。增量序列可有下列取法:
{\displaystyle d_{i}=1,2,3...(m-1)}称为 线性探测(Linear Probing);即{\displaystyle d_{i}=i},或者为其他线性函数。相当于逐个探测存放地址的表,直到查找到一个空单元,把散列地址存放在该空单元。
{\displaystyle d_{i}=\pm 1^{2},\pm 2^{2},\pm 3^{2}...\pm k^{2}}{\displaystyle (k\leq m/2)}称为 平方探测(Quadratic Probing)。相对线性探测,相当于发生冲突时探测间隔{\displaystyle d_{i}=i^{2}}个单元的位置是否为空,如果为空,将地址存放进去。
{\displaystyle d_{i}=}伪随机数序列,称为 伪随机探测。
显示线性探测填装一个散列表的过程:
- 关键字为{89,18,49,58,69}插入到一个散列表中的情况。此时线性探测的方法是取
{\displaystyle d_{i}=i}。并假定取关键字除以10的余数为散列函数法则。
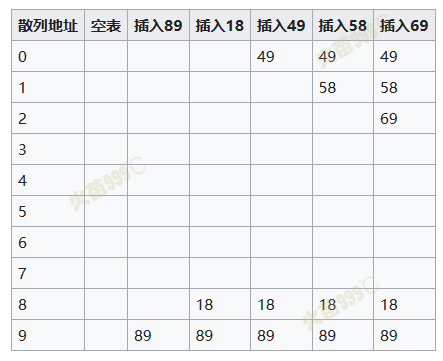
- 第一次冲突发生在填装49的时候。地址为9的单元已经填装了89这个关键字,所以取
{\displaystyle i=1},往下查找一个单位,发现为空,所以将49填装在地址为0的空单元。第二次冲突则发生在58上,取{\displaystyle i=3},往下查找3个单位,将58填装在地址为1的空单元。69同理。 - 表的大小选取至关重要,此处选取10作为大小,发生冲突的几率就比选择质数11作为大小的可能性大。越是质数,mod取余就越可能均匀分布在表的各处。
聚集(Cluster,也翻译做“堆积”)的意思是,在函数地址的表中,散列函数的结果不均匀地占据表的单元,形成区块,造成线性探测产生一次聚集(primary clustering)和平方探测的二次聚集(secondary clustering),散列到区块中的任何关键字需要查找多次试选单元才能插入表中,解决冲突,造成时间浪费。对于开放定址法,聚集会造成性能的灾难性损失,是必须避免的。
- 单独链表法:将散列到同一个存储位置的所有元素保存在一个链表中。实现时,一种策略是散列表同一位置的所有冲突结果都是用栈存放的,新元素被插入到表的前端还是后端完全取决于怎样方便。
- 双散列。
- 再散列:
{\displaystyle hash_{i}=hash_{i}(key)},{\displaystyle i=1,2...k}。{\displaystyle hash_{i}}是一些散列函数。即在上次散列计算发生冲突时,利用该次冲突的散列函数地址产生新的散列函数地址,直到冲突不再发生。这种方法不易产生“聚集”(Cluster),但增加了计算时间。 - 建立一个公共溢出区
例程
在C语言中,实现以上过程的简要程序:
开放定址法:
// HashTable
InitializeTable(int TableSize) {
HashTable H;
int i;
// 為散列表分配空間
// 有些编譯器不支持為struct HashTable 分配空間,聲稱這是一個不完全的結構,
// 可使用一个指向HashTable的指針為之分配空間。
// 如:sizeof(Probe),Probe作为HashTable在typedef定義的指針。
H = malloc(sizeof(struct HashTable));
// 散列表大小为一个質数
H->TableSize = Prime;
// 分配表所有地址的空間
H->Cells = malloc(sizeof(Cell) * H->TableSize);
// 地址初始為空
for (i = 0; i < H->TableSize; i++)
H->Cells[i].info = Empty;
return H;
}查找空单元并插入:
// Position
Find(ElementType Key, HashTable H) {
Position Current;
int CollisionNum;
// 冲突次数初始为0
// 通過表的大小對關鍵字進行處理
CollisionNum = 0;
Current = Hash( Key, H->TableSize );
// 不為空時進行查詢
while (H->Cells[Current].info != Empty &&
H->Cells[Current].Element != Key) {
Current = ++CollosionNum * ++CollisionNum;
// 向下查找超過表範圍時回到表的開頭
if (Current >= H->TableSize)
Current -= H->TableSize;
}
return Current;
}- 分离连接法
查找效率
散列表的查找过程基本上和造表过程相同。一些关键码可通过散列函数转换的地址直接找到,另一些关键码在散列函数得到的地址上产生了冲突,需要按处理冲突的方法进行查找。在介绍的三种处理冲突的方法中,产生冲突后的查找仍然是给定值与关键码进行比较的过程。所以,对散列表查找效率的量度,依然用平均查找长度来衡量。
查找过程中,关键码的比较次数,取决于产生冲突的多少,产生的冲突少,查找效率就高,产生的冲突多,查找效率就低。因此,影响产生冲突多少的因素,也就是影响查找效率的因素。影响产生冲突多少有以下三个因素:
- 散列函数是否均匀;
- 处理冲突的方法;
- 散列表的载荷因子(英语:load factor)。
载荷因子
散列表的载荷因子定义为:{\displaystyle \alpha }= 填入表中的元素个数 / 散列表的长度
{\displaystyle \alpha } 是散列表装满程度的标志因子。由于表长是定值,{\displaystyle \alpha } 与“填入表中的元素个数”成正比,所以,{\displaystyle \alpha } 越大,表明填入表中的元素越多,产生冲突的可能性就越大;反之,{\displaystyle \alpha } 越小,标明填入表中的元素越少,产生冲突的可能性就越小。实际上,散列表的平均查找长度是载荷因子{\displaystyle \alpha }的函数,只是不同处理冲突的方法有不同的函数。
对于开放定址法,荷载因子是特别重要因素,应严格限制在0.7-0.8以下。超过0.8,查表时的CPU缓存不命中(cache missing)按照指数曲线上升。因此,一些采用开放定址法的hash库,如Java的系统库限制了荷载因子为0.75,超过此值将resize散列表。
举例:Linux内核的bcache
Linux操作系统在物理文件系统与块设备驱动程序之间引入了“缓冲区缓存”(Buffer Cache,简称bcache)。当读写磁盘文件的数据,实际上都是对bcache操作,这大大提高了读写数据的速度。如果要读写的磁盘数据不在bcache中,即缓存不命中(miss),则把相应数据从磁盘加载到bcache中。一个缓存数据大小是与文件系统上一个逻辑块的大小相对应的(例如1KiB字节),在bcache中每个缓存数据块用struct buffer_head记载其元信息:
struct buffer_head {
char *b_data; // 指向缓存的数据块的指针
unsigned long b_blocknr; // 逻辑块号
unsigned short b_dev; // 设备号
unsigned char b_uptodate; // 缓存中的数据是否是最新的
unsigned char b_dirt; // 缓存中数据是否为脏数据
unsigned char b_count; // 这个缓存块被引用的次数
unsigned char b_lock; // b_lock表示这个缓存块是否被加锁
struct task_struct *b_wait; // 等待在这个缓存块上的进程
struct buffer_head *b_prev; // 指向缓存中相同hash值的下一个缓存块
struct buffer_head *b_next; // 指向缓存中相同hash值的上一个缓存块
struct buffer_head *b_prev_free; // 缓存块空闲链表中指向下一个缓存块
struct buffer_head *b_next_free; // 缓存块空闲链表中指向上一个缓存块
};整个bcache以struct buffer_head为基本数据单元,组织为一个封闭定址(close addressing,即“单独链表法”解决冲突)的散列表struct buffer_head * hash_table[NR_HASH]; 散列函数的输入关键字是b_blocknr(逻辑块号)与b_dev(设备号)。计算hash值的散列函数表达式为:
(b_dev ^ b_blocknr) % NR_HASH
其中NR_HASH是散列表的条目总数。发生“ 冲突”的struct buffer_head,以b_prev与b_next指针组成一个双向(不循环)链表。bcache中所有的struct buffer_head,包括使用中不空闲与未使用空闲的struct buffer_head,以b_prev_free和b_next_free指针组成一个双向循环链表free_list,其中未使用空闲的struct buffer_head放在该链表的前部。
原文地址:
https://zh.wikipedia.org/wiki/%E5%93%88%E5%B8%8C%E8%A1%A8
在知识共享 署名-相同方式共享 3.0协议之条款下提供