在计算机科学与数学中,一个排序算法(英语:Sorting algorithm)是一种能将一串资料依照特定排序方式排列的算法。最常用到的排序方式是数值顺序以及字典顺序。有效的排序算法在一些算法(例如搜索算法与合并算法)中是重要的,如此这些算法才能得到正确解答。排序算法也用在处理文字资料以及产生人类可读的输出结果。基本上,排序算法的输出必须遵守下列两个原则:
- 输出结果为递增序列(递增是针对所需的排序顺序而言)
- 输出结果是原输入的一种排列、或是重组
虽然排序算法是一个简单的问题,但是从计算机科学发展以来,在此问题上已经有大量的研究。举例而言,冒泡排序在1956年就已经被研究。虽然大部分人认为这是一个已经被解决的问题,有用的新算法仍在不断的被发明。(例子:图书馆排序在2004年被发表)
分类
在计算机科学所使用的排序算法通常依以下标准分类:
- 计算的时间复杂度(最差、平均、和最好性能),依据列表(list)的大小(
{\displaystyle n})。一般而言,好的性能是{\displaystyle O(n\log n)}(大O符号),坏的性能是{\displaystyle O(n^{2})}。对于一个排序理想的性能是{\displaystyle O(n)},但平均而言不可能达到。基于比较的排序算法对大多数输入而言至少需要{\displaystyle O(n\log n)}。 - 内存使用量(以及其他电脑资源的使用)
- 稳定性:稳定排序算法会让原本有相等键值的纪录维持相对次序。也就是如果一个排序算法是稳定的,当有两个相等键值的纪录
{\displaystyle R}和{\displaystyle S},且在原本的列表中{\displaystyle R}出现在{\displaystyle S}之前,在排序过的列表中{\displaystyle R}也将会是在{\displaystyle S}之前。 - 排序的方法:插入、交换、选择、合并等等。
稳定性
当相等的元素是无法分辨的,比如像是整数,稳定性并不是一个问题。然而,假设以下的数对将要以他们的第一个数字来排序。
{\displaystyle (4,1)(3,1)(3,7)(5,6)}
在这个状况下,有可能产生两种不同的结果,一个是让相等键值的纪录维持相对的次序,而另外一个则没有:
(3,1)(3,7)(4,1)(5,6)}(維持次序)
(3,7)(3,1)(4,1)(5,6)}(次序被改變)不稳定排序算法可能会在相等的键值中改变纪录的相对次序,但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。作这件事情的一个方式是人工扩展键值的比较,如此在其他方面相同键值的两个对象间之比较,(比如上面的比较中加入第二个标准:第二个键值的大小)就会被决定使用在原先资料次序中的条目,当作一个同分决赛。然而,要记住这种次序通常牵涉到额外的空间负担。
排序算法列表
在这个表格中,{\displaystyle n}是要被排序的纪录数量以及{\displaystyle k}是不同键值的数量。
稳定的排序
冒泡排序(bubble sort)— {\displaystyle O(n^{2})}
插入排序(insertion sort)—{\displaystyle O(n^{2})}
鸡尾酒排序(cocktail sort)—{\displaystyle O(n^{2})}
桶排序(bucket sort)—{\displaystyle O(n)};需要{\displaystyle O(k)}额外空间
计数排序(counting sort)—{\displaystyle O(n+k)};需要{\displaystyle O(n+k)}额外空间
归并排序(merge sort)—{\displaystyle O(n\log n)};需要{\displaystyle O(n)}额外空间
原地归并排序— {\displaystyle O(n\log ^{2}n)}如果使用最佳的现在版本
二叉排序树排序(binary tree sort)— {\displaystyle O(n\log n)}期望时间;{\displaystyle O(n^{2})}最坏时间;需要{\displaystyle O(n)}额外空间
鸽巢排序(pigeonhole sort)—{\displaystyle O(n+k)};需要{\displaystyle O(k)}额外空间
基数排序(radix sort)—{\displaystyle O(nk)};需要{\displaystyle O(n)}额外空间
侏儒排序(gnome sort)— {\displaystyle O(n^{2})}
图书馆排序(library sort)— {\displaystyle O(n\log n)}期望时间;{\displaystyle O(n^{2})}最坏时间;需要{\displaystyle (1+\varepsilon )n}额外空间
块排序(block sort)— {\displaystyle O(n\log n)}
不稳定的排序
选择排序(selection sort)—{\displaystyle O(n^{2})}
希尔排序(shell sort)—{\displaystyle O(n\log ^{2}n)}如果使用最佳的现在版本
克洛弗排序(Clover sort)—{\displaystyle O(n)}期望时间,{\displaystyle O(n^{2})}最坏情况
梳排序— {\displaystyle O(n\log n)}
堆排序(heap sort)—{\displaystyle O(n\log n)}
平滑排序(smooth sort)— {\displaystyle O(n\log n)}
快速排序(quick sort)—{\displaystyle O(n\log n)}期望时间,{\displaystyle O(n^{2})}最坏情况;对于大的、随机数列表一般相信是最快的已知排序
内省排序(introsort)—{\displaystyle O(n\log n)}
耐心排序(patience sort)—{\displaystyle O(n\log n+k)}最坏情况时间,需要额外的{\displaystyle O(n+k)}空间,也需要找到最长的递增子序列(longest increasing subsequence)
不实用的排序
Bogo排序— {\displaystyle O(n\times n!)},最坏的情况下期望时间为无穷。
Stupid排序—{\displaystyle O(n^{3})};递归版本需要{\displaystyle O(n^{2})}额外存储器
珠排序(bead sort)— {\displaystyle O(n)}或 {\displaystyle O({\sqrt {n}})},但需要特别的硬件
煎饼排序—{\displaystyle O(n)},但需要特别的硬件
臭皮匠排序(stooge sort)算法简单,但需要约{\displaystyle n^{2.7}}的时间
简要比较
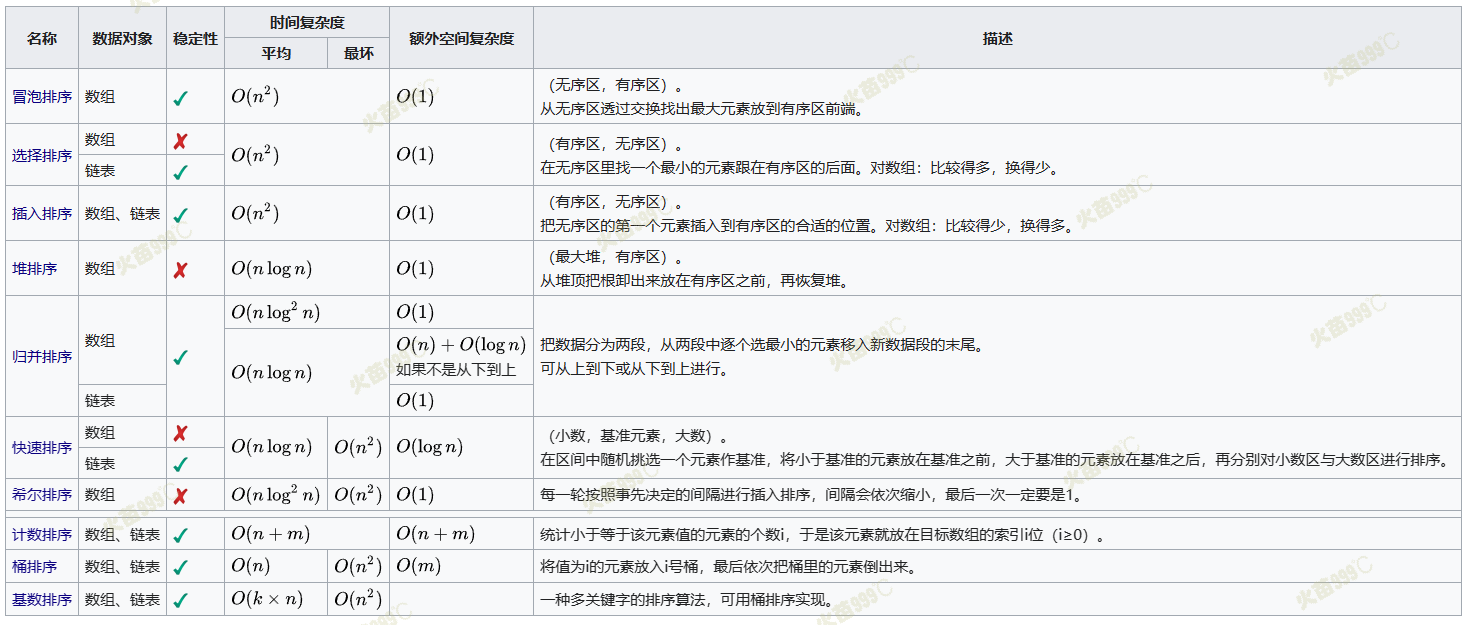
- 均按从小到大排列
- k代表数值中的"数位"个数
- n代表数据规模
- m代表数据的最大值减最小值
原文地址:https://zh.wikipedia.org/wiki/%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95
在知识共享 署名-相同方式共享 3.0协议之条款下提供
